Instead of going in order of my units, I decided to start with some of my faves first. I love factoring and I love how I progress through factoring. Hopefully eventually I'll do a vlog (never done one)/video talking you through how I build coherence through multiplying, factoring, and dividing - but until then, here's how I initially progress through factoring. I use the box/area/partial products method for factoring, so students are already used to using that framework.
My order:
Finding a GCF
Factoring out a GCF ("skinny box" AND intro factoring GCF from a 2x2 box)
Difference of Squares (this could also go at the end after trinomials)
Factoring trinomials where a = 1 ("X factor", aka just sum/product puzzles if you know those)
Factoring trinomials where a isn't 1 ("X Box" originally inspired by Julie at ispeakmath.)
Factoring completely
First thing is we need to establish what a GCF is and how to find it, which is part of a class period. The rest of the day we talk about factoring out a GCF from a polynomial by putting each term into a compartment of the hence forth "skinny box".
The same day and the beginning of the next we talk about factoring out of a 2x2 box. I think this is one of the key elements that helps my students be so successful later when we do trinomials. Hint: I used to teach this part as finding the GCF of each row/column but now just have them find the GCF of the first row and then go around saying what times (GCF) gives me whats in the box? Works SO much better now and works seamlessly with the intuition for dividing polynomials with the box in Math 3 (coherence!!!)
The next day we move onto Difference of Squares - next semester I might move this to the end. Stole the note form from Sarah Carter at mathequalslove. My twist with this is my "Difference of Squares" rap. While I haven't video taped it. I guess someone in my class recorded this and entitled it "When Math Teachers Try to Make Class Fun" <3 . Before direct instruction I have them multiply out several difference of squares to notice/wonder about the pattern.
Me doing it (slower than I usually do so they can see the steps)
Brave student then doing it for the class (LOVE HER!)
It's ridiculously cheesy but one of the best feelings later when the students learn it and you have a whole class getting into it with you. =)
Next up is trinomials where a is one which I affectionately call the "X Factor"...because you use an X, and you are factoring...and I love puns, especially if they are terrible.
I give students a sum/product puzzle where at first all the numbers are given and I ask them to find a pattern that works for all the Xs. (Love introing things as a puzzle, because isn't that really all factoring is?! and you get more interest/buy in from students when you present it this way). We then talk about how to use this method to factor. Once we move onto where a isn't 1 we talk about why it always starts with (x ) (x ) if your a is 1.
Then we move onto X Box. To start this off, I give them a filled in box and have them find the GCF and all the sides like we did Day 1. How was that? "Easy" then I have them do an X Factor problem. How was that? "Easy" I then write up the original polynomial we started with and ask them to notice/wonder about where the different numbers and terms are coming from in the original polynomial so that they practically discover the process for themselves. Thanks to Elissa @misscalcul8 for typing up my notes!
By the way, throughout all of this I'm constantly emphasizing that factoring is just rewriting a problem as multiplication.
Last, we factor completely. For that I made a handy dandy flow chart because, let's face it, I <3 flow charts.
Here's the link to my documents that I've actually created. I will add others to the same link as I get around to typing them up! Sorry for the awful handwritten copies for now, but hey - something is better than nothing!
Here are my old youtube videos explaining it if you are still curious. Notes: I was still doing the GCF for all rows/column method in the X Box Video =/
GCF:
Difference of Squares:
X Factor
X Box:
SIDE NOTE: I actually am changing things up a bit by introducing solving by factoring/zero product property first and then practicing with every new method. I found this semester that it really helped students distinguish between what "factor" and "solve" meant!






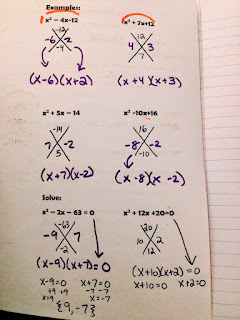






Thanks for sharing. I like the idea of using solving all the way through. It also gives a reason for why we factor.
ReplyDeletePlease follow up how that goes.