While I lurked for a couple years and then started my blog over a year ago - I don't think I was really part of the #MTBoS community until going to #TMC14. Since TMC14 I have experienced so much love and support. I have been going through hell in my personal life the last 2 years, and I can honestly say the the MTBoS has been a great support for me, even though no one knows that I have been going through anything. Friends are always there to encourage, bounce ideas off of, lament the many struggles of teaching, and to push you forward to become the best teacher you can be. With their support I think I have developed so much professionally the past year that I know I would not have been able to do alone. Teaching can be such an isolating profession, especially if you are trying innovative - or just different - ideas. The MTBoS lets you see that there are others like you, who understand what you are trying to do and will try to help or at least encourage you along the way. There is always something new to learn and someone to push back and help you refine your thinking. I only hope that as time goes on I can offer that kind of support and encouragement to other teachers. - especially young teachers, who like me have big dreams of teaching mathematics but not all the resources or know-how as a newbie.
So if you are out there lurking, don't be shy! I learned a lot by lurking, but so much more by becoming actively involved, especially on Twitter. Come join this amazing, nerdy, and supportive family as you journey on your path of teaching. =)
Friday, July 17, 2015
Sunday, July 12, 2015
Unit 4: Radical Rationals
I love introducing this unit using Sam Shah's Introduction to Rationals, basically every day of teaching it I pace around like a mad woman (more than usual) getting progressively more and more excited as time goes on. At least it adds a little theatrics to what could otherwise feel pretty dry and boring. I felt like I truly understood rationals the first time I worked through his introductions myself.
So we spend a couple days on that (I just briefly touch on slant asymptotes since I'm not required to do that yet, but I of course freak out over how we can find them easily using...the Box - yes I need a 12 step program for this obsession).
We then take off with
Graphs of Rationals:
I just wrote out my own notes this semester because I didn't like the ones I used before and we got to the graphing part before I typed any up. We did some basic graph practice - honestly, I have no idea where I got that worksheet.
The right hand page they do a sorting activity with VA and HA. I got it from TPT (gasp) back in my first year of teaching.
Multiply/Dividing Rationals
Some basic notes
Then they did a showdown activity where first they had to sort whether the problem was multiplication or division.
Adding/Subtracting Rationals
Some more basic notes
A basic matching activity
And then adding/subtracting speed dating!
Solving Rationals
Then we lose our minds when we get to solving. Next time I will type up these notes. Copying the equations takes 10 years.
I split up practice over two days. After notes they did this simple matching worksheet. Then they did a solving Around the World activity. Yay for finding what you are looking for and not having to make it yourself.
Solving Radicals
Then we randomly talk about radical equations because hey, why not?
I've got some lovely guided notes for you.
Then I spontaneously decided to do a different kind of practice with cards I had made before for speed dating. I color coded them (duh) green for easy/entry level, yellow for moderate and red for challenging. Students self-assessed where they were and then worked on problems in that group, moving up or down as necessary. I was completely shocked that I ended up needing several more of the hardest problems because students really grasped the concept and wanted to push themselves. They got very into the activity and I want to try incorporating it more somewhere else. I pulled problems from several locations for the activity and don't have a doc for them =/ sorry.
Unit resources link:
So we spend a couple days on that (I just briefly touch on slant asymptotes since I'm not required to do that yet, but I of course freak out over how we can find them easily using...the Box - yes I need a 12 step program for this obsession).
We then take off with
Graphs of Rationals:
I just wrote out my own notes this semester because I didn't like the ones I used before and we got to the graphing part before I typed any up. We did some basic graph practice - honestly, I have no idea where I got that worksheet.
The right hand page they do a sorting activity with VA and HA. I got it from TPT (gasp) back in my first year of teaching.
Multiply/Dividing Rationals
Some basic notes
Then they did a showdown activity where first they had to sort whether the problem was multiplication or division.
Adding/Subtracting Rationals
Some more basic notes
A basic matching activity
And then adding/subtracting speed dating!
Solving Rationals
Then we lose our minds when we get to solving. Next time I will type up these notes. Copying the equations takes 10 years.
I split up practice over two days. After notes they did this simple matching worksheet. Then they did a solving Around the World activity. Yay for finding what you are looking for and not having to make it yourself.
Solving Radicals
Then we randomly talk about radical equations because hey, why not?
I've got some lovely guided notes for you.
Then I spontaneously decided to do a different kind of practice with cards I had made before for speed dating. I color coded them (duh) green for easy/entry level, yellow for moderate and red for challenging. Students self-assessed where they were and then worked on problems in that group, moving up or down as necessary. I was completely shocked that I ended up needing several more of the hardest problems because students really grasped the concept and wanted to push themselves. They got very into the activity and I want to try incorporating it more somewhere else. I pulled problems from several locations for the activity and don't have a doc for them =/ sorry.
Unit resources link:
Unit 3: Polynomial Party
I'd be lying if I said I didn't love teaching polynomials. Maybe it is because it is one of those units where a lot of previous topics start coming together, but in any case - I love it. In the spring the first part of the unit started off while we were having a million snow days so luckily it transitioned well to students completing at home with my videos, but we didn't get to do some of the fun activities I made. However I have still included them.
Add/Subtract/Multiply Polynomials
At this point students have added and subtracted any polynomials, but have only multiplied as high as binomials times a trinomials. This is where we step it up a notch and where my love of the box comes out in full style. Usually in class I would be doing some sort of excited dance about the box because I know what is coming the next day...DIVIDING W/ the Box...but holding on:
Notes:
Right Hand:
Bull's eye worksheet. They add the first circle, then subtract, then multiply to what is on the side. Good discussion of order and whether we are always going back to the original. If we had been in class we would have practiced with dice I made with different polynomials written on them. Then roll a die 1,2 means add them, 3,4 means subtract, and 5,6 means multiply.
Divide Polynomials
I've already written a blog post here* about how I teach dividing. It is my favorite thing ever. Check it out =). I've included the pics here again. If it hadn't been a snow day then we would have done a Showdown activity found here. To learn how to play the game look here*.
Remainder Theorem
This page is one of my efforts to turn something boring like a simple worksheet into a sorting activity. I just formatted a kuta worksheet to be just the polynomials. Students then sorted whether they were factors/roots or not. At first I was going to make a big stink about factors vs. roots...but I didn't hold to it very well. Oops. Also the green = yes a factor/root....red = no. Because color with purpose = <3
Factoring Completely Given Known Factor
Typed up some lovely notes.
Then they did a speed dating activity to practice.
Rational Root Theorem
More wonderful notes. I wasn't super evil in making them use trial and error to find the roots. We just talked about them being the only possible rational ones and then found the right ones on the graphing calculator.
I had this beautiful idea for an activity for the day. Since they were going to be solving polynomials and sometimes there are multiple ways, ie factoring vs graphing or maybe quadratic formula vs completing the square when they get to the end I thought it would work well for an activity I heard at a conference. You give each group an envelope with a problem on the front., When they finish, they put the problem solution in the envelope and pass it on. The next group tries without looking at prior groups' responses and at the end the last group looks at all the answers and chooses the one they like the most. So great...however...I did not feel it that day so they ended up just doing the problems. C'est la vie.
Problems found here. I was of course proud of the nifty little book I got them to make.
Irrational and Imaginary Root Theorem/Write Eq from Roots
I loved the changes I made to this section after seeing this from Denis Sheeran.
First we did some notes about irrational and imaginary root theorems. I really need to emphasize better the benefit of the theorem is that we can always use the POSITIVE conjugate when writing equations like on the right hand page. Otherwise their brain tends to explode with the squaring a negative is a positive, but i^2 is -1...etc.
Root Theorem Notes
Writing EQ Given Roots Notes
Writing EQ Around the World Activity (Answer sheet, activity)
Graphs of Polynomials
I like Meg Craig (@mathymeg) could spend 200 million years talking about graphing polys. I love them. I started with students sorting graphs according to common features. I used the cards from Julie at ispeakmath that she adapted from Amy at Square Root of Negative One Teach Math. They sorted the graphs first, then we talked about the features and they matched the word cards to them. Of course, typical Type-A style we fit them into a table and then summarized the table on the front. On the back we took notes on how to sketch.
Then we did a version of speed dating. I put problems of either graphing or writing an eq from a graph on a pair of desks. Students rotated through all of the pairs. For the group with the writing an eq from graph they were given a strip of labels to write the answers on so that the cards effectively turned into flash cards.
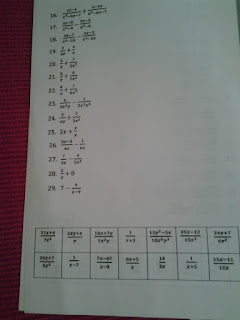
For the sketching problems I formatted this page with just the equations. For writing the equations I used a worksheet I can't find...If I run across it I will add it here.
Thanks for coming to the Polynomial Party =)
Here is the box info for the whole unit link:
Add/Subtract/Multiply Polynomials
At this point students have added and subtracted any polynomials, but have only multiplied as high as binomials times a trinomials. This is where we step it up a notch and where my love of the box comes out in full style. Usually in class I would be doing some sort of excited dance about the box because I know what is coming the next day...DIVIDING W/ the Box...but holding on:
Notes:
Right Hand:
Bull's eye worksheet. They add the first circle, then subtract, then multiply to what is on the side. Good discussion of order and whether we are always going back to the original. If we had been in class we would have practiced with dice I made with different polynomials written on them. Then roll a die 1,2 means add them, 3,4 means subtract, and 5,6 means multiply.
Divide Polynomials
I've already written a blog post here* about how I teach dividing. It is my favorite thing ever. Check it out =). I've included the pics here again. If it hadn't been a snow day then we would have done a Showdown activity found here. To learn how to play the game look here*.
Remainder Theorem
This page is one of my efforts to turn something boring like a simple worksheet into a sorting activity. I just formatted a kuta worksheet to be just the polynomials. Students then sorted whether they were factors/roots or not. At first I was going to make a big stink about factors vs. roots...but I didn't hold to it very well. Oops. Also the green = yes a factor/root....red = no. Because color with purpose = <3
Factoring Completely Given Known Factor
Typed up some lovely notes.
Then they did a speed dating activity to practice.
Rational Root Theorem
More wonderful notes. I wasn't super evil in making them use trial and error to find the roots. We just talked about them being the only possible rational ones and then found the right ones on the graphing calculator.
I had this beautiful idea for an activity for the day. Since they were going to be solving polynomials and sometimes there are multiple ways, ie factoring vs graphing or maybe quadratic formula vs completing the square when they get to the end I thought it would work well for an activity I heard at a conference. You give each group an envelope with a problem on the front., When they finish, they put the problem solution in the envelope and pass it on. The next group tries without looking at prior groups' responses and at the end the last group looks at all the answers and chooses the one they like the most. So great...however...I did not feel it that day so they ended up just doing the problems. C'est la vie.
Problems found here. I was of course proud of the nifty little book I got them to make.
Irrational and Imaginary Root Theorem/Write Eq from Roots
I loved the changes I made to this section after seeing this from Denis Sheeran.
First we did some notes about irrational and imaginary root theorems. I really need to emphasize better the benefit of the theorem is that we can always use the POSITIVE conjugate when writing equations like on the right hand page. Otherwise their brain tends to explode with the squaring a negative is a positive, but i^2 is -1...etc.
Root Theorem Notes
Writing EQ Given Roots Notes
Writing EQ Around the World Activity (Answer sheet, activity)
Graphs of Polynomials
I like Meg Craig (@mathymeg) could spend 200 million years talking about graphing polys. I love them. I started with students sorting graphs according to common features. I used the cards from Julie at ispeakmath that she adapted from Amy at Square Root of Negative One Teach Math. They sorted the graphs first, then we talked about the features and they matched the word cards to them. Of course, typical Type-A style we fit them into a table and then summarized the table on the front. On the back we took notes on how to sketch.
Then we did a version of speed dating. I put problems of either graphing or writing an eq from a graph on a pair of desks. Students rotated through all of the pairs. For the group with the writing an eq from graph they were given a strip of labels to write the answers on so that the cards effectively turned into flash cards.
For the sketching problems I formatted this page with just the equations. For writing the equations I used a worksheet I can't find...If I run across it I will add it here.
Thanks for coming to the Polynomial Party =)
Here is the box info for the whole unit link:
Subscribe to:
Comments (Atom)